Метод скінченних різниць. Параболічні рівняння

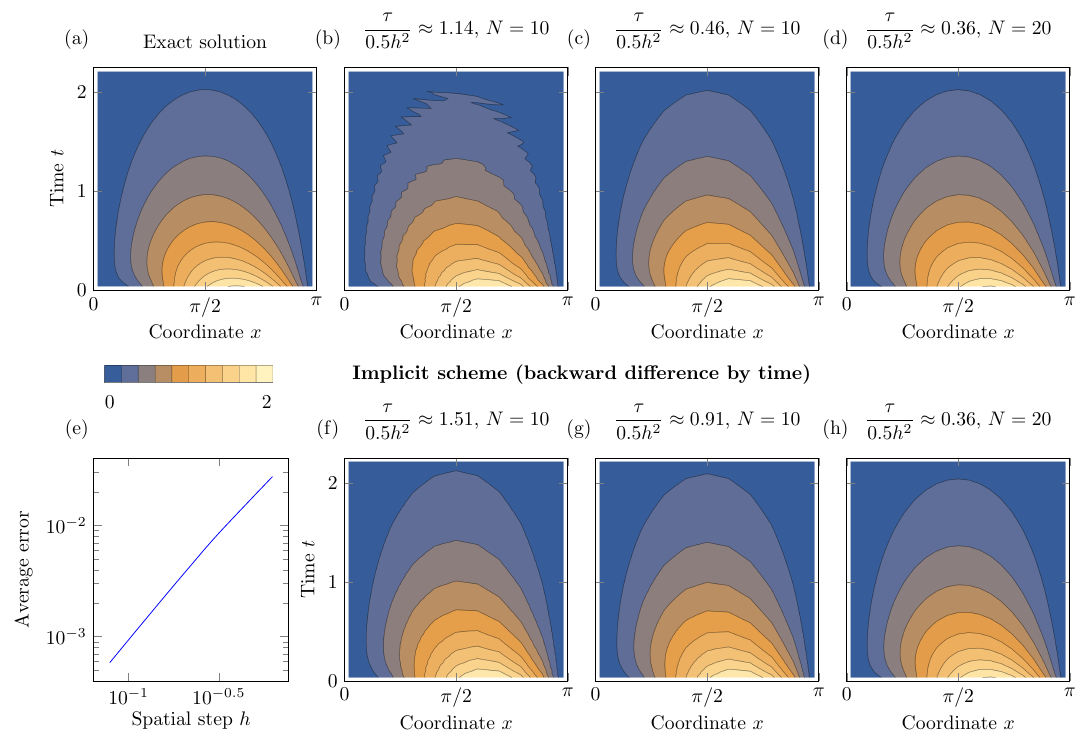
Явна схема

$$\partial_{xx}u + f(x,t) = \partial_t u , \quad x \in [0, L],\quad u(0, t) = \mu_0(t), \quad u(L,t) = \mu_1(t), \quad u(x, 0) = g(x).$$

Прямокутна сітка по простору-часу з кроками h (індекс i) і tau (індекс j) відповідно.

$$\dfrac{u_{i,j+1} - u_{i,j}}{\tau} = \dfrac{u_{i+1,j} - 2u_{i,j} + u_{i,j}}{h^2} + f_{i,j},\quad i=\overline{1,N-1},j=\overline{0,M-1}$$

$$u_{0,j} = \mu_0(j\tau),\quad u_{N,j} = \mu_1(j\tau),\quad u(i,0) = g(ih)$$

Єдине невідоме:

$$u_{i,j+1} = u_{i,j}{\tau} + \dfrac{\tau}{h^2}(u_{i+1,j} - 2u_{i,j} + u_{i,j}) + \tau f_{i,j}$$

$$\dfrac{\tau}{h^2} < 0.5$$

Неявна схема

$$\dfrac{u_{i,j+1} - u_{i,j}}{\tau} = \dfrac{u_{i+1,j+1} - 2u_{i,j+1} + u_{i,j+1}}{h^2} + f_{i,j+1},\quad i=\overline{1,N-1},j=\overline{0,M-1}$$

Методи Рунге-Кутти

$$\partial_t \vec{u} = \vec{f}(t, \vec{u}, \partial_x \vec{u}, \ldots),\quad \vec{u}(t=0) = \vec{u}_0(x)$$

$$\vec{u}(t+\tau) = \vec{u}(t) + \tau \partial_t \vec{u}(t) + \dfrac{\tau^2}{2} (\partial_t^2\vec{u}(t))^2 + \ldots$$

Для оцінки попереднього виразу розглянемо розклад функції f в ряд Тейлора:

$$\vec{f}(t+\tau, \vec{u} + \tau\vec{k}) = \vec{f}(t,\vec{u} ) + \tau \partial _t\vec{f}(t,\vec{u} ) + \partial_{\vec{u}} \vec{f}\times (\tau \vec{k})$$

Друга похідна від u за часом:

$$\partial_t^2\vec{u}(t) = \partial_t (\partial_t\vec{u}) = \partial_t (\vec{f})$$

Виконавши математичні перетворення, отримаємо

$$\vec{u}(t+\tau) = \vec{u}(t) + \dfrac{\tau}{2}(\vec{k}_1 + \vec{k}_2)$$

$$\vec{k}_1 = \vec{f}(t, \vec{u}), \quad \vec{k}_2 = \vec{f}(t+\tau, \vec{u} + \tau \vec{k}_1)$$

.